오늘의 논문 링크: https://arxiv.org/pdf/1802.04712.pdf
Attention-based Deep Multiple Instance Learning , 2018
multiple instance learning (MIL) 란, 의료영상과 같이 annotation이 약하고, ROI(region of interest)가 대략적인 데이터들을 학습할 때 발생되는 문제들을 해결하기위해 고안되었다(e.g., computational pathology, mammography or CT lung screening) .
이는 의존성과 규칙성이 없는 bag of instances를 하나의 클래스로 정의 하고, 모델이 이를 학습하여 bag of instances 를 예측하는 문제를 다룬다. 하지만 기존의 bag-level classifier 들은 instance level 정확도가 낮고, 일반적으로 instance level 에서는 MIL 에 포함된다고 볼 수 없었다.
Introduction
In this paper, we propose a new method that aims at incorporating interpretability to the MIL approach and increasing its flexibility.
저자들은 MIL 모델을 베루누이 분포를 통한 bag label 로 접근하였다. 또한, log-likelihood funcion을 활용한 학습을 통해 이를 최적화한다.
* 베루누이 분포 : 이항분포에서 n=1 일때. 즉, 결과가 binary인 실험이나 시행(베르누이 시행) 의 결과를 실수 0과 1로 바꾼 확률 변수 분포. 만약 어떤 확률 변수 X 가 베르누이분포에 의해 발생된다면 " 확률변수 X 가 베루누이 분포를 따른다" 라고 된다. 주사위를 한번만 던진것.
Bag label probability( the bag score function ) 을 모델링하기위해 다음 세가지 절차를 보여준다
- 저차원 임베딩으로의 인스턴스 변환
- 순열 불변(단순) 집계 함수
- Bag probability에 대한 최종 변환.
그리고 학습은 유연한 접근 및 End-to-end 로 모델 최적화된 학습이 가능한 neural networks를 활용하였고, max, mean 연산과 같이 널리 사용되는 순열 불변 연산자를 Attention mechanism (Bahdanau et al., 2014; Raffel & Ellis, 2015)에 부합하는 두개의 학습가능한 레이어를 가진 NN의 가중치의 weighted average로 대체함을 제안한다.
주목할 점은, attention weights가 key instances를 찾아서, ROI들을 강조하는데 추가적으로 사용할 수 있도록 하는것이다.
Methodology
일반적인 Binary task에서는 추론값이 다음과 같다. 주어진 인스턴스 x 값에 대해 추론값 y는 0과 1로 분류된다.

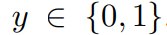
하지만 MIL task에서는 하나의 인스턴스가 아닌 여러개의 bag of instances 들을 다룬다. 이들은 서로간의 의존성도, 어떠한 질서도 없다. 또한, 내부에 담긴 instance갯수들 또한 다양할 것으로 추정한다. 이 bag에 대한 binary label 인 Y 는 하나로 정의된다.
더 나아가, bag 을 구성하는 각각의 instance들에 대한 레이블 또한 추정한다. y_1, y_2 ..., y_k 까지, 그러나 이는 학습 도중에는 알 수 없으며 이를 통해 MIL problem의 Y를 가정하는 수식을 다음과 같이 쓸수있다.


이러한 가정은 MIL 모형이 순열 불변이어야 한다는 것을 의미한다. 즉, 인풋 instance들의 순서와 상관없이 output이 같아야한다는 뜻이다.
하지만 인스턴스 레이블에 대한 최댓값을 기반으로 모델을 학습하는 것은 다음 두 가지 이유로 문제가 될 수 있다고 한다.
첫번째로, 고질적인 문제인 vanishing gradients 와 두번째로는 이 공식은 instance level classifier 만이 적합하게 사용될수 있다는 점이다.
In order to make the learning problem easier, we propose to train a MIL model by optimizing the log-likelihood function where the bag label is distributed according to the Bernoulli distribution
때문에 본 논문에서는 MIL 문제를 log-likelihood function으로 모델 최적화를 할 수 있도록, bag of instances 로 부터 probability of Y=1 의 파라미터를 통한 베르누이 분포를 활용한다.
MIL 문제 공식에서 두 정리의 점수 함수는 확률 γ(X)와 순열 불변이다. 함수 σ을 MIL pooling이라고 한다. f, g 및 σ 함수의 선택에 따라 레이블 확률 추정의 접근법으로 특정된다. 주어진 MIL 연산자에 대해 두 가지 주요 MIL 접근법이 있다.
1) The instance-level approach : f 는 말그대로 각각의 instance마다 score를 반환하는 instance-level classifier 를 사용한다. 그리고 θ(X)를 구하기위해 MIL pooling 로 집계한다. g 는 identity function 이 된다.
2) The embedding-level approach : 여기서 f는 instance들을 low-dimensional embedding으로 만든다. MIL pooling을 통해서는 각각의 독립적인 수의 instance들의 bag representation을 얻기위해 사용된다. 그리고 이 bag representation(feature)은 bag-level classifier 를 통해 θ(X) 를 얻는다.

저자들은 새로운 MIL Pooling을 사용하여 해석 가능한 Embeding-level approach 를 제안한다.
MIL pooling
MIL problem은 순열불변의 법칙때문에 MIL pooling σ 을 필요로한다.
대표적으로 maximum operator와 mean operator 가 있고, 이 외에도 convex maximum, noisy-or, noisy-and 등이 있다.


제안되는 새로운 MIL pooling은 max operation을 대신할 수 있고, 또 이러한 연산방식은 차별화될수 있으므로 손쉽게 NN 구조의 연산모듈로써 사용가능하다.

Attention-based MIL pooling
Attention mechanism
instance접근법 에서는 max operation은 좋은 옵션이 되지만 embedding입장에서는 부적절하다. mean또한 마찬가지, 따라서 평균 가중치 of instances(low-dimensional embeddings) 을 사용한다. 이때 가중치는 총 합이 1이여야한다. (bag 사이즈의 불균형 때문에) activation으로는 hyperbolic tangent를 사용하였다.이는 인스턴스간의 유사도를 판단 할 수 있게 한다. H = {h1, . . . , hK} 는 bag of K embeddings다. e w ∈ R^(L×1) and V ∈ R^(L×M) 는 파라미터.
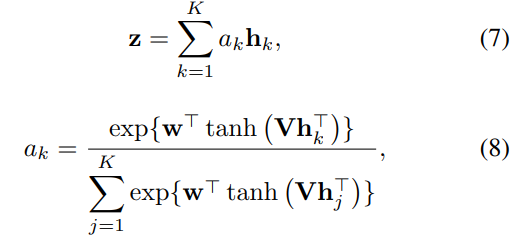
Gated attention mechanism
복잡한 관계성들을 학습하기에는 tahn function이 효과적이지 못한 것을 발견하여 gating mechanism 을 추가하게 되었다.

Experiments
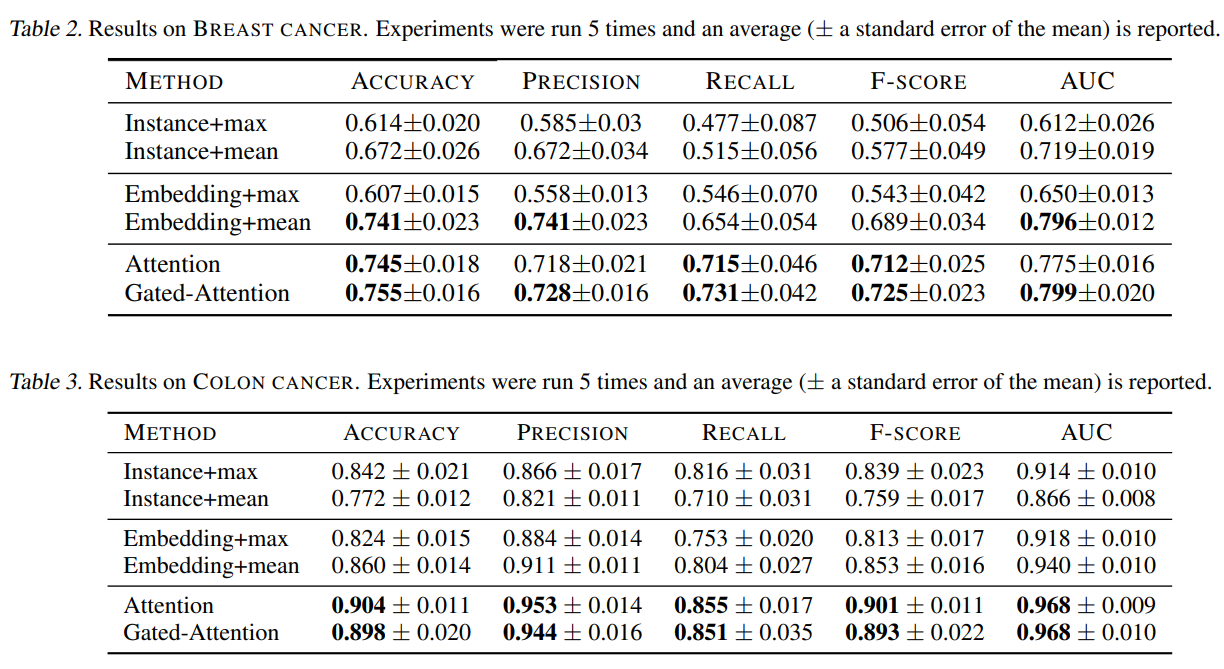
눈여겨 볼 점은 attention mechanism이 ROI를 제공하는데 있어 유용하게 활용 될 수 있을것이라는 점이다. 다음 그림과 같이 attention 가중치에 상응하는 패치들을 겹쳐 만든 히트맵(d)을 보면 gt (c) 와 유사한것을 볼 수 있다.


또, 위 그림에서 instance-based classifier는 단 하나의 적은 positive patch subset 을 선택하는 경향이 있다. 이는 instance 접근법의 낮은 instance accuracy를 확증한다.
오늘은 새롭게 Multiple Instance Learning에 대해 알아보았다. MIL은 방대한 픽셀을 가지고, 매우 불규칙한 세포단위의 특징들을 다루게 되는 의료 영상처리로 주로 연구되어지고 있는 분야였다. 또, attention에 대한 중요도를 다시한번 느끼게되었다. 이 논문은 실험적인 부분에서 매우 흥미롭게 잘 기술되어있어서 평소보다 재밌게 읽었던 듯 하다.
fin.
@article{ITW:2018,
title={Attention-based Deep Multiple Instance Learning},
author={Ilse, Maximilian and Tomczak, Jakub M and Welling, Max},
journal={arXiv preprint arXiv:1802.04712},
year={2018}
}